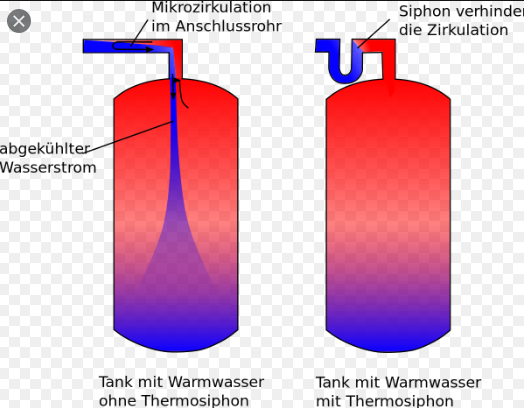
More insulation is obviously better.
We are both talking about storing energy more efficiently, but using two different mechanisms.
Let’s do some sums, with a few assumptions.
The ambient temperature and the cold water is 15 deg C.
The geyser heats a volume of 100L to 60 deg C.
(Fact: It takes about 4.2kJ/kg (ltr) to heat water/degree).
Energy needed (60-15) 45 * 4.2kJ* 100 + losses = 18900kJ
1J/sec = 1 watt. 3600J = 1 watt/hour, therefore 18900kJ = 5.25kWh
I deal with losses later.
With me so far?
OK, @plonkster’s paper talked about 2kWh of leat loss/ day. (I’ll stick with that number).
So our 60-degree water if left alone, will have lost 7200kJ.
(Note 1: This is not strictly true because the study wouldn’t have left it alone but replenished the losses through the thermostat function, but let’s work with this number because it is what we have).
That 7200kJ loss is an indication of the quality of the insulation. A geyser blanket will improve the quality of the insulation and make those losses less in a 24hr period.
There is no way around supplying the energy needed to heat the material. But in my special case, I don’t care about that because it comes from the sun. What I care about is needing to replace that 2kWh of energy from my battery, and the cost and inefficiencies in that process because I want hot water the next morning and the sun hasn’t been shining for the last 12 hours of the night.
I am getting my energy very cheaply and efficiently, but I only have 18900-7200 = 11700kJ left of what I stored as thermal energy.
My thermal energy storage (11700/18900) is only 62% efficient.
Right, now I am going to strip the insulation of a similar geyser and fit it in a Jojo tank with 210 L of my phase change 56 C degree paraffin.
I am going to assume the same quality of insulation, but there is a bigger area so let’s say the losses are now double 4kWh/day. ( guessing here, but you’ll see they could still be a lot higher and this would work).
I come along with my free solar energy in the day and I have to expend the same amount of energy to heat the water 5.25kW/h.
So far so good.
But now I need to heat up that paraffin as well. (Fact: It takes about 2.5kJ/kg (ltr) to heat paraffin/degree).
So 210 litres * 45deg * 2.5kJ/kg = 23625 kJ or 6.56kWh of sensible heat.
Why do I call it “sensible” heat?
Sensible heat is actually a real term that is used to mean the type of heat that changes the temperature of a substance. It is the opposite of latent heat, which does not change temperature only the state of the substance.
So we have to factor in the latent heat we had to supply to the solid paraffin to melt it at 56 degrees.
(Fact: It takes about 236kJ/kg (ltr) to melt paraffin 26 at 56.3 degrees).
That is 236 * 210 = 49560kJ = 13.77 kWh.
So to heat up my geyser takes 5.25 + 6.56 + 13.77 = 25.58kW/h.
Ah, but I am now having to make 25.58kW, not 5.25kW everybody cries!
-No you’re not, you are just storing that amount, you don’t have to make it every day, just build up to it, you only have to replace what you use. It’s just like having more batteries, doesn’t mean you use more power.
Ah, but I am losing 4kWh, not 2kWh everybody cries!
-True, but consider it further:
I have 21.58kWh stored energy the next day. My storage efficiency is now (21.58/25.58)= 84%.
What’s more in the first example my water temperature would have theoretically have dropped 17 degrees,( see Note 1 above), whereas using PCM it will still be 56 degrees.
In fact, the maths would show that cold water could be added the next day and without any solar the next day and it would still heat up to 56 degrees. No insulation in the world could do that.
Ah, but paraffin is a nasty chemical and flammable, I don’t want it around my water supply or electrics, everybody cries!
True, I am calling it paraffin because that is what it is. It is flammable, but not explosive, you may be more familiar with its use in your load-shedding candles. It is a chemical yes, it’s that red coating on your cheese. It’s wax and it is also an excellent electrical insulator. Please don’t stop eating gouda or candles on birthday cakes.
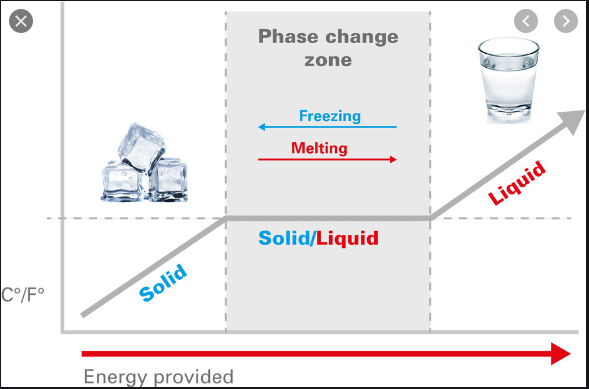
It is a bit difficult to get your head around, a liquid having so much more energy than a solid at the same temperature.
Maybe this pic will help, just think of that flat line at 56 degrees.
There is the same amount of energy transfer that happens in ice>water as is needed to heat that glass of water to 80 deg C.
It’s quite mad actually, and it works in both directions. For example, I could use typical night-time temperatures to freeze a substance at say 15C, and then run a fan through it, instead of an AC in the daytime for cooling.