I know 4mm is cheaper and 6mm can carrey higher current, but at what stage should you opt for 6mm and when is 4mm sufficient?
There are various online calculators:
Here is one:
(Remember cable length is there and back).
Always 6mm. I don’t want to have to pull more cable later… At all.
Worth the extra cost.
Not sure what the current pricing is like since everything is crazy these days.
When I installed 2-3 years ago, cable was still cheap and the difference between 4mm and 6mm wasn’t really much so I just used 6mm on 3 of my strings.
When I added the last, I couldn’t find 6mm so I used 4mm. These are on sunsynk inverters so 1p, meaning crazy overkill.
Easier to fit 4 x 4mm^2 through 20mm conduit… but other than that… 6mm^2 all the way. Can’t remember the last time I used the thinner stuff.
I, too, standardized on 6mm, because it is the largest size that fits a standard MC4 connection.
Then I ran the cabling at 30A per spur.
However, the next installation I plan on will be weighted with AC-coupled PV inverters, with perhaps only 1 or 2 external MPPT charge controllers.
Then I will run most of my PV as single series strings just below 600V with some pretty long runs.
I think 4mm cabling might offer me quite a cost-saving at an acceptable performance penalty.
I think the efficiency price should be weighed against the price of extra panels.
Can I make more watts with cheaper cabling and extra panels?
The panels can roughly produce 12-13 amps nowadays. If you string 4 of them the current stays the same. 2.5mm can handle 25Amps, 4mm can handle 32A and 6mm can handle 40A.
So the current does not matter in this case. You can use 2.5mm for 12 amps, the determining factor is the volt drop. So the further you go, the bigger the cable. I did two examples below. Sans require you to stay below 5% volt drop but in Solar you want to design the system to be below a 3% volt drop and in solar farms they specify the volt drop to remain below 1%.
With your system the string voltage is low so the voltage drop is much higher than with sunsynk where we can string 8 panels or even a Fronius where we normally string 16 panels. On a sunsynk for example I can use 2.5mm pv wire per 8 panel string up to 40 meters and we remain below 3% volt drop.
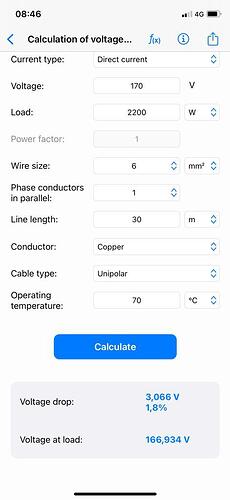
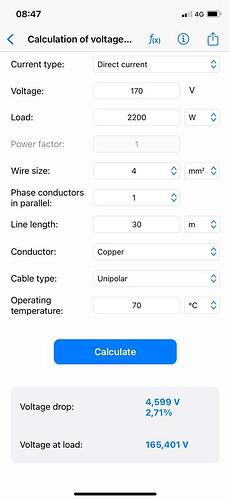
The example below is based on 4s 550 watts with an operational voltage of approximately 170VDC.
As can be seen with 6mm you’ll have a volt drop of 1.8% and with 4mm you’ll have 2.71%
So again, its not about the current carrying capacity of the cable, the panel can only supply a certain current, the cable size gets determined by the length of the string and volt drop in this application.
Interesting statement. Can you please tell us why?
Uuuh, if you’re working out total voltage drop over the length of cable, it must be over the whole length. So if your panels are 5 meters away, then you have 5 meter of positive and 5 meter of negative cable, for a total of 10m cable. At least I think that is what he means?
Doing the calculation over only half the distance is an easy mistake to make.
Found this statement…hmm
‘The circuit length is from the beginning point to the end point of the circuit regardless of the number of conductors.’
So now what do these voltage drop apps use?
Exactly why I asked the question.
If you work it out yourself, you have to make sure your doing the right thing. Apps normally have a selection of cables, so when using an app, makes sure about the selections, if you select single core, double the length to your panels. I you have the option for a multicore cable, the app will do the calc.
The app I use show no difference in volt drop between Unipolar and multipolar as it assumes the load is X meter from the source and 2 wires are needed to complete the circuit.
So my question was a suspicious, but I just wanted to clarify this. Make sure of what your app offers and don’t double the length if its not needed.
After a quick discussion with my friend, that’s where the confusion is. A lot of the apps on the internet already takes this into account, especially where multicore cable is involved. When you have multiple conductors tied together, the current rating is slightly lower as they also tend to heat each other and dissipate the heat more poorly.
But if you have the raw ohms per meter figure, with PV cable, and working from basic principles, you have to take the total length when you calculate the voltage drop.
For that reason I’m actually not very fond of the apps.
Not that it matters too much. The point we’re making is that you pick the 6mm cable not only for the higher current capacity, but also for the lower voltage drop, and it is very easy to “flunk that test” if you forget that the length might be longer than it looks.
(The Afrikaans “dop daai toets” sounds so much more funny for when someone makes a mistake like this ![]() ).
).
Yes, I think you both understood what I meant.
Another point to add, perhaps, is that the current capacity is proportional to the SQUARE of the diameter. Pi times radius squared. So a 6mm^2 cable isn’t just 50% bigger. It’s 125% bigger!
(Same thing happens in plumbing. A 110mm sewage pipe has more than twice the capacity of a 70mm gutter pipe, and the 70mm gutter pipe has 3 times the capacity of a 40mm pvc waste pipe ![]() ).
).
The area, in this case 6mm² is related to the SQUARE of the diameter in the same way…
So the diameter of a 6mm² cable is not 50% bigger than that of a 4mm², but rather only ~22.5%.
I love this forum!!! ![]()
Similarly, the standing loss in one 200l geyser is much than in two 100l geysers combined. Making it easier and the geysers cubes, a square block with a volume of 27 units^3 has a surface area of 54 units^2, while a square block with a volume of 64 units has a surface area of 96 units^2. So you more than double your capacity but less than double your surface area. (This effect naturally gets bigger as the sizes increase)
There’s that question with the somewhat surprising answer: If you imagine the earth as a massive round ball, and you have a rope that goes perfectly around the earth’s surface, how much longer should the rope be if you want it to make a circle 1m higher than the surface of the earth.
Well, the circumference is 2πr, so the extra length is 2πΔr, and Δr = 1, so you need 2π meter more rope, or just over 6 meters.
Indeed, which seems surprising initially, right? ![]()
What surprises me now, is having gone through so many notches on my belt.